A considerable number of dynamical systems in engineering practice are essentially hybrid in nature. These systems model non-smooth phenomena such as impact, collision, and switching between discrete modes. The orbits of such systems are typically characterized by smooth evolutions, interrupted by discrete jumps, making the analysis of the state-space inherently more complicated. For these systems, the traditional interpretation of the state-space geometry in terms of individual trajectories may not offer much insight, and it is useful to consider the evolution of ensembles of initial conditions instead.
In this research project, we take a “set-oriented” viewpoint to hybrid systems by characterizing their behavior through the spectral properties of the Koopman operator. The applications of Koopman operator theory have been quite profound in the analysis of smooth nonlinear dynamics (particularly in fluid flows). Yet, for systems that exhibit discontinuous phenomena the use of the theory has been relatively less explored.
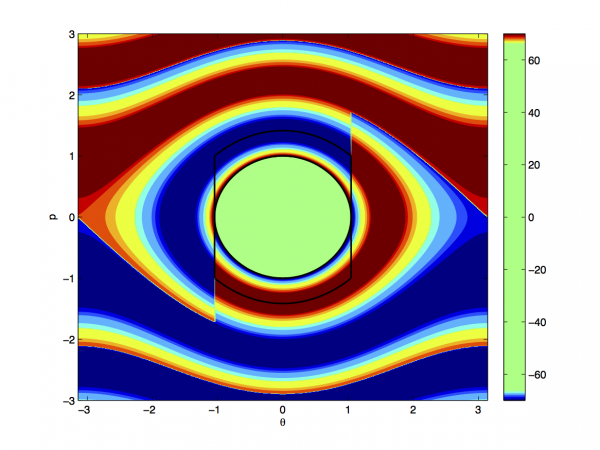
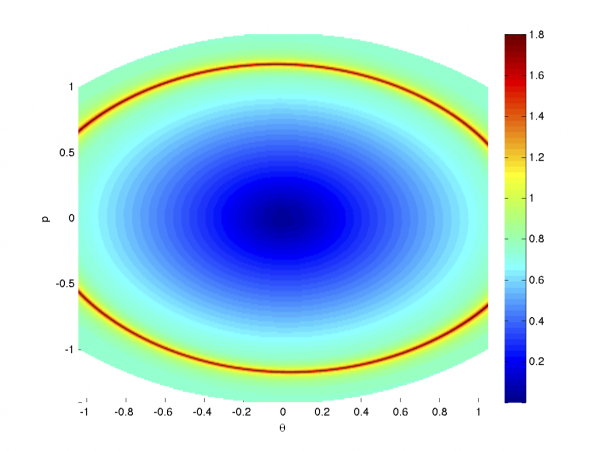
As a step towards venturing into this domain, we have looked into a particular benchmark example of a hybrid pendulum that receives downwardly facing kicks under certain fixed angles. Two cases are considered: (i) an undamped case where the continuous part of the system is Hamiltonian, and (ii) a damped case where the Hamiltonian vector field is perturbed by marginal amounts of viscous damping. In both cases, the eigenfunctions of the Koopman operator provide a meaningful characterization of the state-space geometry. For the undamped system, the eigenfunctions at eigenvalue zero were particularly useful in identifying the basins of the limit cycles (see figure below). For the damped system, certain eigenfunctions of the operator were useful in establishing a (semi-)conjugacy with a much simpler linear system.
Papers related to this research project:
N. Govindarajan, H. Arbabi, L. van Blargian, T. Matchen, E. Tegling, and I. Mezic. An operator-theoretic viewpoint to non-smooth dynamical systems: Koopman analysis of a hybrid pendulum. Submitted to CDC 2015